SPANC -- SPlitpole ANalysis Code User Manual
Author: Dale Visser; Date: 14 January 2002
Functional Description of Code
Spanc is a code created by Dale Visser for easier calibrations of position spectra from magnetic spectrometer experiments. In particular, it was created for use at Yale University for analyzing spectra from our Enge spectrometer. In Spanc, the user enters descriptions of the targets and reactions used in an experiment. Then, they enter information about peaks which are to be used for calibration of the spectra. Spanc can then fit the calibration peaks with polynomials of order 1 thru 4. ρ is fitted as a function of spectrum channel. The user can then enter additional peaks, along with which reaction they are associated with. Spanc will return back estimates of ρ and excitation energy, based on the calibration curve. Spanc can save input data, calibration info, and output data to a file, which can then be loaded back in later on. Also, Spanc can save a report to a text file of the input data, calibration, and output data.
How to Use Spanc
A typical session of Spanc goes as follows:
- Enter information about targets.
- Enter information about reactions.
- Enter information about calibration peaks.
- Select a polynomial fit order.
- Enter output peaks, and see results.
Detailed instructions on each of these steps follows.
Entering Target Information
Select the 'List Targets...' option from the Targets menu. This displays the 'Target List' dialog box. To add a new target, click the button 'Add' in this dialog box. A 'Define Target' dialog box appears. By default, this dialog box shows information for a 20 μg/cm2 carbon target. If this is what is desired, all that is necessary is to give it a name, and click 'OK'.
The target definition table in the 'Define Target' dialog has one row for each layer in a target. Layer 0 is the first layer the beam encounters, and each successive Layer number is the next layer downstream. Layers may be added by clicking 'Add Layer'. This adds a layer to the end of the list, which is given a default value of 20 μg/cm2 of carbon. If you click on a row, and then click 'Remove Layer', that layer gets removed from the table.
The 'Components' cell for a layer may be edited to specify what elements are in the layer in what proportions. The format is simple. For each element, type an element symbol (upper/lower case does matter) followed by a space and a number. The numbers should represent the relative numbers of atoms of each element in the target. For example, silicon dioxide would be entered as "Si 1 O 2". The 'Thickness' cell for a layer may be edited to give the thickness in μg/cm2 for that layer.
Clicking 'OK' or 'Apply' creates the target object. It will now be listed in the 'Target List' dialog box. Selecting one of the targets in the list, and clicking 'Display' will display a 'Display Target' dialog. In it, you will see the target as you defined it. Note that the numbers for each element will be renormalized to a total of 1. I recommend that you always display a target after creating it, in order to double check that it was created properly.
Targets may be deleted by selecting them in 'Target List', and clicking 'Remove'.
Entering Reaction Information
A reaction in Spanc is specified by a beam nuclide, beam energy, spectrometer B-field, target, interaction layer, target nuclide, projectile nuclide, projectile charge state, and spectrometer angle. All this information may be entered for a new reaction by clicking 'Add Reaction' in the 'Calibration Reactions' section of the main window. This displays an 'Add Reaction' dialog.
The 'Beam' and 'Projectile' fields are for specifying the nuclides. In them, you must enter the nuclide in the form AAAZZZ, where AA is the mass number of the nucleus, and ZZZ is the element symbol. For example, silicon-29 would be entered as "29Si". The beam energy is entered in MeV, and the B-field is entered in kG. The target is specified by choosing one of your entered targets from a dropdown list. The layer that your reaction is assumed to occur in must then be selected from the 'Layer' slider. 'Target Nuclide' is a drop-down list containing all known isotopes of elements in your chosen target layer. Select the desired isotope. Q is an integer representing the charge state of your projectile. Finally, the angle of the spectrometer must be entered in degrees.
For every nuclide participating in the reaction, it is possible to specify the mass as having uncertainty. When calibrating an experiment internally, i.e. using well known calibration peaks from the same reaction as the output peaks, the masses can be treated as exact. However, when different reaction channels are used for calibrating, any different reactants and products should have their mass uncertainties counted.
Clicking 'OK' or 'Apply' creates the reaction, and adds it to the 'Calibration Reactions' table in the main window. Each reaction has a number associated with it in the 'Reaction' column, which you will use when specifying calibration peaks and output peaks. Selecting a row in the reaction table, and clicking 'Remove Reaction' will delete a reaction from the list.
Entering Calibration Peak Information
Calibration peaks in Spanc are specified by a reaction, a projectile excitation energy, a residual excitation energy, and a centroid channel. To add a calibration peak, click 'Add Peak' in the 'Calibration Peaks' section of the main window. This displays an 'Add Calibration Peak' dialog.
Select which reaction the peak belongs to using the 'Reaction' slider. You must do this at least once, even if it appears that your desired reaction is already selected. Enter an excitation energy in MeV for the projectile. A default value of 0 is already present. Projectile excitation energies are assumed to be exact in Spanc at the present time. Enter the residual excitation energy in MeV in the 'Ex Residual [MeV]' field, and the uncertainty in keV in the 'Ex Residual Unc. [keV]' field. These units were chosen because they are the standard units used in the Table of Isotopes. In the next two fields, enter the centroid channel for your peak, and its uncertainty.
Clicking 'OK' or 'Apply' creates the peak, and adds it to the 'Calibration Peaks' table in the main window. ρ is calculated automatically for the peak, along with an uncertainty based on entered residual excitation energy. If any reaction participant nuclides have been specified as having mass uncertainty (see the section on entering reaction information), their mass uncertainties are also included in ρ's uncertainty. Spanc, like all of my nuclear physics codes, gets its nuclear masses from the 1995 evaluation by Audi and Wapstra [1] (as provided by the file mass_rmd.mas95 available at http://csnwww.in2p3.fr/AMDC/web/amdcw_en.html).
Spanc assumes that the nuclear interaction point in the target is exactly halfway through the specified interaction layer. Beam energy loss is calculated up to this point (for normal incidence), and used as the beam energy in the 2-body kinematics calculation. The projectile has its energy loss through the remainder of the target. The projectile energy loss uses the exit angle out of the target into the spectrometer. The final projectile energy after exiting the target is reflected in the reported ρ value. Energy losses are calculated using the formulas given in Ziegler [2].
Performing a Fit
Spanc performs linear regressions to fit ρ as a function of channel using polynomial. The polynomials may be 1st order thru 4th order. The dependence fit is as follows:
ρ = a0 + a1 (Channel - Channel[0]) + a2 (Channel - Channel[0])2 + ...
Channel[0] is simply the unweighted mean of all the calibration peak channels. It is exact, and not really a parameter of the fit. Rather, it is a constant shift of the data made in order to reduce the covariance between the a0 and a1 terms. (In an unweighted 1st-order linear regression, this transformation actually eliminates the covariance.) The value of Channel[0] is displayed all the way to the right in the 'Fit' section..
To perform a fit, simply slide the 'Fit Order' slider to the desired order of polynomial you would like to use. Spanc displays the degrees of freedom in the 'd.o.f.' box, and requires that there be at least one degree of freedom before it will perform a fit. When performing a fit, Spanc first assumes the channels (x-axis) to be exact, and performs a weighted fit using the ρ error bars (y-axis). This is a standard linear regression with error bars in the y-axis. It then uses this fit as an approximation to determine an effective contribution of the channel error bars in the y-axis (fit slope at channel × channel error bar). This gets added in quadrature with the given y-error bar to give an effective y-error bar. A second fit is performed with these effective y-error bars.
'ChiSq/d.o.f.' contains the calculated value of the χ2 statistic for the fit, divided by degrees of freedom. The expectation value for the χ2 distribution is the number of degrees of freedom. Therefore, for good fits, you expect to see a value for 'ChiSq/d.o.f.' near 1. The 'p-value' field contains the tail probability of the χ2 distribution for this fit. It is the probability that 'ChiSq/d.o.f.' would be equal to or greater than the present calculated value if the fit does, in fact, represent the true calibration curve. Ideally, it should be greater than 0.90 or 0.95, but anything above 0.5 should be OK, in my opinion. The true check of the goodness-of-fit is to take a look at the residuals, which are listed in the second table in the 'Fit' section. The 'Resid./Sigma' column uses the effective y-error bars calculated for the fit. If the fit is good, about 2/3 of the values in this column should be less than 1. One wouldn't expect more than about one in twenty values to be greater than 2.
The fitted parameters, along with their associated error bars are listed in the first table in the 'Fit' section. The error bars are simply the square of the appropriate diagonal element in the covariance matrix. The covariance matrix is displayed to the right in the same table.
Entering Output Peaks
Output peaks in Spanc are specified by a reaction, a projectile excitation energy, and a channel. Output peaks are displayed in the bottom section of the main window, and are entered in a very similar fashion to the calibration peaks. Clicking 'Add Peak' in the 'Output Peaks' section displays an 'Add Output Peak' dialog.
Again, you must slide the 'Reaction' slider to the desired reaction number, even if it appears to already be selected. The projectile excitation energy is again presumed to be exact and given a default value of zero, which you may change. Channel number and uncertainty are entered just as with the calibration peaks.
Clicking 'OK' or 'Apply' creates the output peak. If a calibration fit has already been performed, the peak is added to the table in the 'Output Peaks' section. In this table, a fitted value for ρ is displayed. The excitation energy for the residual nucleus is calculated for this ρ by adding back the energy loss to the interaction point in the target, then working the two-body kinematics in reverse. The excitation energy error bar is determined from the ρ, which has its error bar calculated as described below.
Two sources of error are added in quadrature: the channel uncertainty in the output peak, and the prediction interval one gets assuming the output peak channel were known exactly. The former simply comes from multiplying the channel error bar by the slope of the fit function evaluated at the channel. The second is the Prediction Interval, calculated by the following formula:
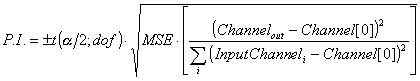
where ![]() and
and 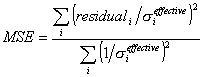
For a t-distribution with r degrees of freedom, the probability for values greater than t(a;r) is equal to a. This t-distribution is the appropriate sampling distribution for the calculated fit values. a in the above expression for the prediction interval is chosen to be 1-0.683, where 0.683 is the probability inside ±1sigma for the standard normal distribution.
Notice that the Prediction Interval has a parabolic form where the prediction uncertainty is lowest at the center of the calibration data.
Adjusted Error Bars
There is a checkbox in the output peaks section for adjusting error bars. If this box is checked and χ2/d.o.f. is greater than 1, the prediction interval error bars get multiplied by the square root of χ2/d.o.f. This is to attempt to compensate for a poor quality calibration by amplifying the uncertainty. It is equivalent to assuming that your calibration peak error bars were under-estimated by a factor which would give the expected value of χ2/d.o.f.=1. This is not a statistically justifiable procedure, but it can come in handy when one is trying to get a rough calibration of a data set.
Saving Data and Creating Reports
In the 'File' menu, you may select 'Save Data...' to save your entered targets, calibration reactions, calibration peaks, and output peaks to a file. 'Load Data' may then be used to load this information back into Spanc. You may also select the 'Text Export...' menu item to create a text file showing all your entered information and calibration results in a human-readable format. The text file gives "Adjusted error bars" for output peaks, which are equal to the prediction interval for "good" fits (χ2/d.o.f.≈1). For χ2/d.o.f.>1, it is modified as discussed in the above section.
References
- G. Audi and A. H. Wapstra, Nuclear Physics A 595 (4), 409 (1995).
- J.F. Ziegler H.H. Andersen, The Stopping and Ranges of Ions in Matter 3 (1977); J.F. Ziegler H.H. Andersen, The Stopping and Ranges of Ions in Matter 5 (1977).